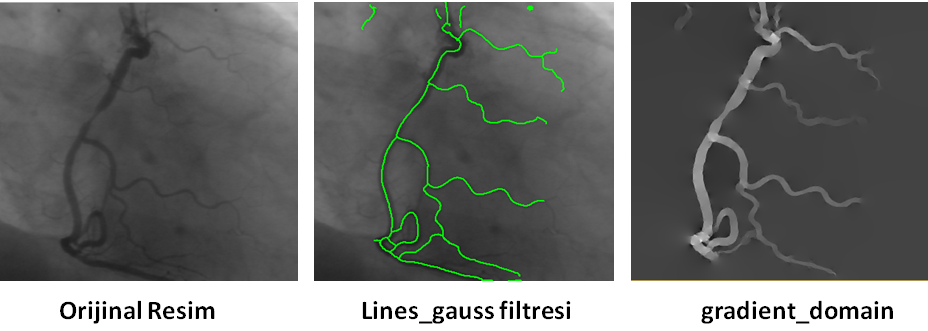
Uzunca bir süredir eni konu bahsetmek istediğim ama bir türlü elimin gitmediği, son yılların en çok araştırılan, üzerinde en çok çalışılan, bir o kadar da bilinmeyen (pek yaygınlaşamayan) görüntü işleme konularından biri olan, Gradient Domain konusuna girmek, bugüne nasip oldu. Başlayalım bakalım…
Ön Bilgi
Resim (Fotoğraf) matematiksel olarak bir çok farklı biçimde modellenebilir / gösterilebilir. Bunlardan en yaygın kullanılanı S-domain sunumu olan spatial domain ismi verilen sunumdur. Bu hepimizin bildiği, her bir pixelin intensity (ışık şiddet / gray value) değerini tuttuğu notasyondur.
Normalde sık sık kullandığımız threshold işlemleri v.b. çoğu fonksiyon, işte bu spatial domain verileri üzerinden işlem yaparlar. Burada, her bir pixel bağımsız olarak ele alınır. Örneğin, tamamen beyaz (gri değeri = 255) olan pixelleri seçmek istiyorsam, bu pixellerin sağına soluna bakmadan, 255 değere sahip olan her bir pixel seçilir.
Tam bu noktada, gradient domain farklı bir yaklaşım sunar. Her bir pixelin tam ve kesin değeriyle ilgilenmek yerine, o pixele komşu olan diğer pixeller ile arasındaki farkı da göz önüne alarak bir matematiksel model bulmaya çalışır. Şimdi her bir pixel değerinin bir öncesi dediğimiz zaman, işi bir seriye dökmeye ihtiyacımız var demektir. Zaten spatial-domain resim dediğimiz, satır ve sütunlardan oluşan bir matris ya da yatay ya da dikey diziler şeklinde düşünülebilir. Elimizdeki bir dizinin elemanlarının değerleri, belirli bir periyotla ya da belirli bir pattern ile tekrarlanıyorsa bu durumda matematiksel olarak frekas domain (frequency domain) den söz edebilirim. (F-domain) f-domain uzayına geçtiğimizde, tıpkı bir dosyanın sıkıştırılması ve geri açılması algoritmalarında olduğu gibi, pixel değerlerinin belirli bir mantığa göre (pattern) tekrarlanması ve bu tekrar mantığını kullanarak, istediğimde orijinal değerlerine ulaşabilmem garanti edilmiş olur. Bunu yapabilmenin en kolay yolu Fourier Transformu’dur. Elimdeki s-doiamn dizisini (satırlar ya da sütunlar), fourier transformuna (hızlı olsun diye fast fourier çoğu kez) tabi tutarsam, resmi bu kez f-domaine almış olurum.
Şimdi elimizde fourier transformu alınmış bir resim var. Durduk yere neden f-domain ile çalışmaya karar verdik? Çünkü artık elimizde matematiksel olarak modellenmiş bir seri var ve her tür spectral işlemleri (lowpass, highpass, bandpass gibi filtleler, konvolüsyon, laplace açılımları v.b. …) yapabileceğimiz tamamen yeni bir matematiksel uzaya geçmiş bulunuyoruz ve bu sonsuz uzayda dilediğimiz gibi at koşturmanın avantajlarından yararlanalım istiyoruz… (elimizde tek bir pixelin gri değeri vardı, nereden nereye geldik.. f-domain ile dur bakalım sonu nereye varacak 🙂 )
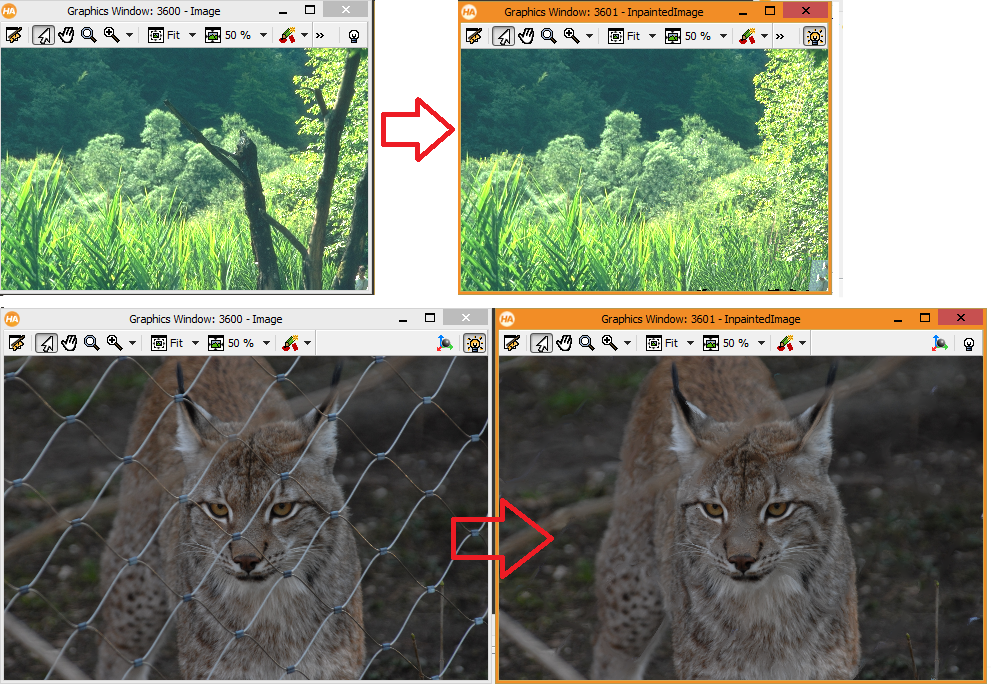
Gradient domain resmi iki bileşenden oluşur. Satır dizisinin türevi alınmış hali Dx, Sütun dizisinin türevi alınmış hali Dy. Dx ve Dy resimlerine bakarsanız, sanki daha çok kenar (edge) çizgileri ile ilgilenmiş gibi? Çünkü her bir pixelin ışık değerinin, komşu pixeller ile olan farkı (türevi) ile ilgileniyor. Tam kenarlarda, ışık değişimi çok daha fazla olduğu için, beklentimize uygun bir sonuç.
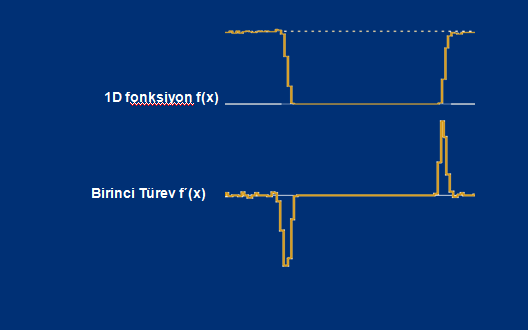Tek boyutlu bir fonksiyonda (dizi) bu fonksiyonun gradient domain fonksiyonu, kısaca onun ilk türevi şeklinde düşünülebilir. (Bu yüzden genelde kenar değerleri pik yapmakta, kenar olmayan, yani ışık şiddetinin değişmediği ya da az değiştiği yerlerde türev sıfır olmaktadır) Gradient domain, eğer spatal domain resminin 1. türevi ise, bu durumda bunun integralini alırsam ne olur? Tabii ki orijinal resme yakın bir resmi elde etmiş olurum.
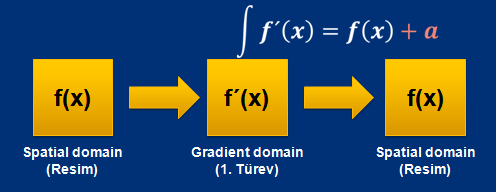
Peki bunca matematiği, dön dolaş başa gelmek için mi yaptık? Tabii ki hayır, o aradaki a katsayısını kaybedebilmek için yaptık.
Yani?
Düşünelim ki, bir resim aldık, doğal olarak bu resmin içinde çeşitli gürültüler (noise) var. Ben orijinal resmi bozmadan, sadece bu gürültüleri nasıl eleyebilirim? Eğer orijinal resim f(x), gürültü a ise, ve benim elimdeki resim de haliyle f(x) + a şeklinde bana gelmiş ise, işte tüm mesele bu a değerini ayıklamaktan ibarettir. Özetle Gradient domain de işte bu işe yaramaktadır. Burada iş yine kolay değildir, çünkü gürültü fonksiyonu, integre edilemeyen bir sabit şeklindedir. Bu yüzden iş biraz biz programcılara düşecektir. Uygun parametreleri vererek sonucu gözlemleyerek, ihtiyacımıza en çok uyan değeri seçeceğiz (Gürültü her resim için sabit olmayacaktır. bazen çok az, bazen çok fazla olabilir. Dolayısıyla, her resimden gürültüyü ele gibi bir fonksiyon beklememekle birlikte, bu eleme işlemi, programcının seçtiği kadar yaptırılabilir)
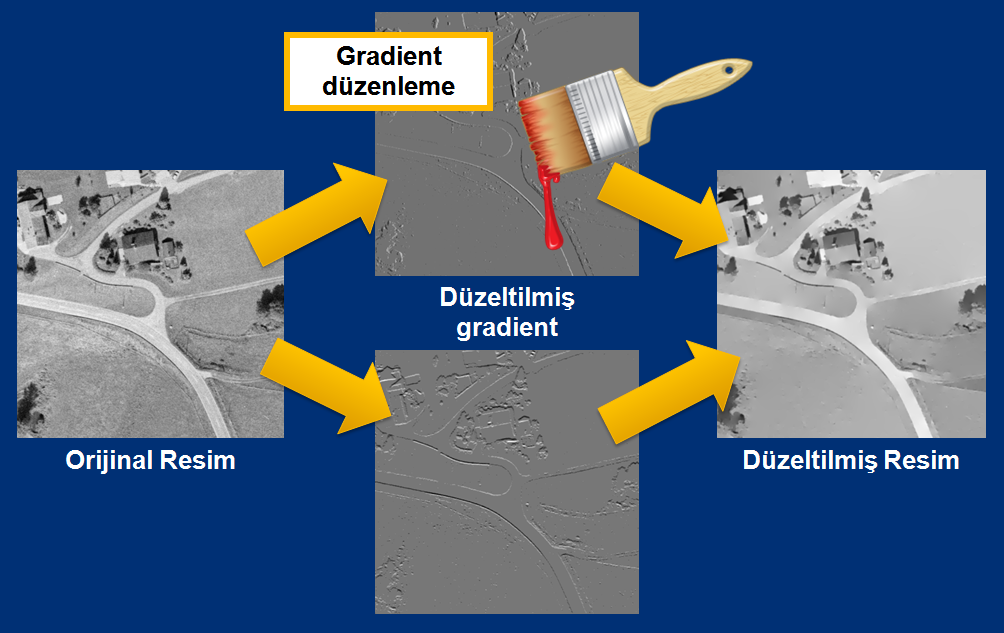Gerçek bir örnekle gösterelim..
Yukarıdaki sonucu test edebileceğiniz HALCON örneğini buradan indirebilirsiniz.
Gradient Domain, filtreleme dışında pek çok alanda kullanılmaktadır. Cep telefonlarımızda bile yer alan HDR işlemi, seamless stitching dediğimiz, bir görüntüyü diğerinin üzerine akıllı olarak yerleştirme, (wikipedia sayfasındaki el üzerine yerleştirilmiş göz resmi resim hayli bilgi verici) kontrast iyileştirme, medikal görüntüleme (x-ray, MR görüntüleri) 3D, color processing, görüntü bindirme gibi alanlarda gittikçe daha sık kullanılmaktadır.
Yukarıda; Termal kamera görüntüsünün, normal kamera görüntüsü ile üst üstebindirilmesi.
Yukarıda; Image Fusion : Görüntülerin üst üste bindirilip, arka planın ve gürültülerin elenmesi.
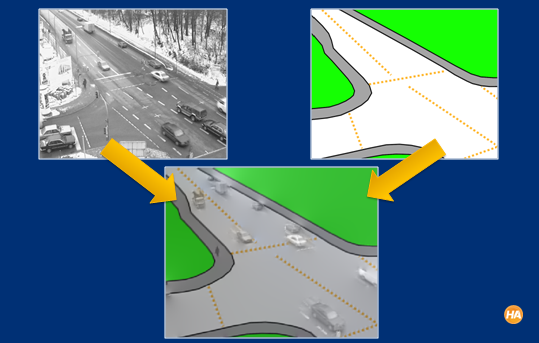Yukarıda; surveillance (trafik) görüntüsünden. Hareket halindeki nesnelerin olduğu bir görüntüde, arka zemini bulabilmek ve ayıklayabilmek oldukça güçtür. Gradient Domain çok iyi sonuç vermiştir.
Özet :
Görüldüğü gibi, hemen her alanda oldukça ilgiçn ve başarılı sonuçlar veren gradient domain üzerine ciddi olarak eğilmek gerekmektedir. Real time processing gerektiren işlemler (Sony TV lerdeki Bravia engine vs.) cep telefonlarındaki kamera uygulamaları (çoğu güncel telefon Sony imx240 sensörünü kullanmaktadır fakat hepsinin son kullanıcıya sunduğu görüntü kalitesi farklıdır, geri planda kullandıkları farklı akıllı algoritmalardan dolayı) fark yaratabilmek için bu ve benzeri teknolojileri kullanmak zorundalar.
Zaman buldukça, kişisel olarak geleceğinin iyi olabileceğini gördüğüm görüntü işleme trendlerine yer vermeyi düşünüyorum.
Görüşmek üzere.
